| Origin: |
It is often attributed to Jean Morlet, engineer at the (late)
French oil company Elf-Aquitaine, now merged within Total (personal note: ELF used to be associated (apocryphally) with Essences et Lubrifiants de France). The
most famous references arise from the collaboration of Alex
Grossman and Jean Morlet, Decomposition of Hardy functions
into square integrable wavelets of constant shape (pdf), SIAM
Journal of Mathematical Analysis, vol. 15, no. 4, pp. 723-736,
July 1984.
Abstract: An arbitrary square integrable real-valued function (or, equivalently, the associated Hardy
function) can be conveniently analyzed into a suitable family of square integrable wavelets of constant shape,
(i.e. obtained by shifts and dilations from anyone of them.) The resulting integral transform is isometric and
self-reciprocal if the wavelets satisfy an "admissibility condition" given here. Explicit expressions are obtained
in the case of a particular analyzing family that plays a role analogous to that of coherent states
(Gabor wavelets) in the usual Lz-theory. They are written in terms of a modified f-function that is
introduced and studied. From the point of view of group theory, this paper is concerned with square
integrable coefficients of an irreducible representation of the nonunimodular ax +b-group
Some earlier works need be mentioned:
- Morlet, J., Arens, G., Fourgeau, I. and Giard, D., Wave
propagation and sampling theory (pdf as part I: Complex signal and scattering in multilayered media and part II: Sampling theory and complex waves ), Geophysics, 47, pp.
203-236, 1982
Abstract: From experimental studies in digital processing of seismic reflection data, geophysicists know that a seismic signal does vary in amplitude, shape, frequency and phase, versus propagation time. To enhance the resolution of the seismic reflection method, we must investigate these variations in more detail.We present quantitative results of theoretical studies on propagation of plane waves for normal incidence, through perfectly elastic multilayered media.As wavelet shapes, we use zero-phase cosine wavelets modulated by a Gaussian envelope and the corresponding complex wavelets. A finite set of such wavelets, for an appropriate sampling of the frequency domain, may be taken as the basic wavelets for a Gabor expansion of any signal or trace in a two-dimensional (2-D) domain (time and frequency). We can then compute the wave propagation using complex functions and thereby obtain quantitative results including energy and phase of the propagating signals. These results appear as complex 2-D functions of time and frequency, i.e., as 'instantaneous frequency spectra.'Choosing a constant sampling rate on the logarithmic scale in the frequency domain leads to an appropriate sampling method for phase preservation of the complex signals or traces. For this purpose, we developed a Gabor expansion involving basic wavelets with a constant time duration/mean period ratio.For layered media, as found in sedimentary basins, we can distinguish two main types of series: (1) progressive series, and (2) cyclic or quasi-cyclic series. The second type is of high interest in hydrocarbon exploration.Progressive series do not involve noticeable distortions of the seismic signal. We studied, therefore, the wave propagation in cyclic series and, first, simple models made up of two components (binary media). Such periodic structures have a spatial period. We present synthetic traces computed in the time domain using the Goupillaud-Kunetz model of propagation for one-dimensional (1-D) synthetic seismograms.Three different cases appear for signal scattering, depending upon the value of the ratio wavelength of the signal/spatial period of the medium.(1) Large wavelengths The composite medium is fully transparent, but phase delaying. It acts like an homogeneous medium, with an 'effective velocity' and an 'effective impedance.'(2) Short wavelengths For wavelengths close to twice the spatial period of the medium, the composite medium strongly attenuates the transmission, and superreflectivity occurs as counterpart.(3) Intermediate wavelengths For intermediate values of the frequency, velocity dispersion versus frequency appears.All these phenomena are studied in the frequency domain, by analytic formulation of the transfer functions of the composite media for transmission and reflection. Such phenomena are similar to Bloch waves in crystal lattices as studied in solid state physics, with only a difference in scale, and we checked their conformity with laboratory measurements.Such models give us an easy way to introduce the use of effective velocities and impedances which are frequency dependent, i.e., complex. They will be helpful for further developments of 'complex deconvolution.'The above results can be extended to quasi-cyclic media made up of a random distribution of double layers. For signal transmission, quasi-cyclic series act as a high cut filter with possible time delay, velocity dispersion, and 'constant Q' type of law for attenuation. For signal reflection they act as a low cut filter, with possible superreflections.These studies could be extended to three-dimensional (3-D) binary models (grains and pores in a porous reservoir), in agreement with well-known acoustic properties of gas reservoirs (theory of bright spots).We present some applications to real well data. Velocity dispersion may explain: mistying between sonic logs and velocity surveys; mistying between synthetic seismograms and seismic sections.Effective velocities lower than mean velocities may explain: very low velocities for P- and S-waves, especially in weathered shallow layers; anomalies on the values of the ratio Vs/Vp ; mistying between P and S seismic sections. Finally, the Gabor expansion provides a tool to obtain sampled instantaneous frequency spectra, and to carry out a suitable recording and processing method in high-resolution seismic, especially to preserve the phase information. Such a processing will involve complex signals, complex traces, complex velocities and complex impedances.For practical purpose, this paper comprises two separate parts. Here, we present some interesting features on the scattering of seismic signals obtained by a simulation method using simple models. We show the usefulness of the notions of complex signals, complex velocities, and complex impedances, and overall of the Gabor expansion, by simulation on very simple models. Morlet et al, (1982, this issue) will be concerned with the development of fundamental notions useful to handle seismic data from the sampling method of recording to processing methods. There we give theoretical and practical tools to sample and handle these data in the time-frequency domain, using complex functions.
Abstract: Morlet et al (1982, this issue) showed the advantages of using complex values for both waves and characteristics of the media. We simulated the theoretical tools we present here, using the Goupillaud-Kunetz algorithm.Now we present sampling methods for complex signals or traces corresponding to received waves, and sampling methods for complex characterization of multilayered or heterogeneous media.Regarding the complex signals, we present a two-dimensional (2-D) method of sampling in the time-frequency domain using a special or 'extended' Gabor expansion on a set of basic wavelets adapted to phase preservation. Such a 2-D expansion permits us to handle in a proper manner instantaneous frequency spectra. We show the differences between 'wavelet resolution' and 'sampling grid resolution.' We also show the importance of phase preservation in high-resolution seismic.Regarding the media, we show how analytical studies of wave propagation in periodic structured layers could help when trying to characterize the physical properties of the layers and their large scale granularity as a result of complex deconvolution. Analytical studies of wave propagation in periodic structures are well known in solid state physics, and lead to the so-called 'Bloch waves.'The introduction of complex waves leads to replacing the classical wave equation by a Schrodinger equation.Finally, we show that complex wave equations, Gabor expansion, and Bloch waves are three different ways of introducing the tools of quantum mechanics in high-resolution seismic (Gabor, 1946; Kittel, 1976, Morlet, 1975). And conversely, the Goupillaud-Kunetz algorithm and an extended Gabor expansion may be of some use in solid state physics.
- Morlet, J., Sampling theory and wave propagation, in
NATO ASI Series, vol. 1, Issues in Acoustics signal/Image
processing and recognition, C. H. Chen (Ed.), Springer Verlag,
pp. 233-261, 1983
Abstract: ###
First known mention of wavelets, as we know them now, by Jean Morlet himself might have been given at a
geophysicist Conference (SEG) in 1975 in Denver, CO, USA, under the title Seismic
tomorrow, interferometry and Quantum Mechanics. A mere 25-line
abstract remains.
Abstract: ###
|
| Anecdote: | The term wavelet is ubiquituous in the field on geosphysics, more
specifically in reflection seismology. It refers to the seismic pulse (once
called impulsion sismique in French) sent through the ground
subsurface in order to detect (after its reflections on interfaces) earth "
structures". Its accurate determination is thus crucial for the wavefield
deconvolution. The word wavelet is attested in early works
such as the one by N. Ricker, A note on the determination of the viscocity
of shale from the measurement of the wavelet breadth, Geophysics, Society
of Exploration Geophysicists, vol. 06, pp. 254-258, 1941.
Abstract: From the breadth of a wavelet for a given travel time, it is possible to calculate the viscosity of the formation through which the seismic disturbance has passed. This calculation has been carried out for the Cretaceous Shale of Eastern Colorado, and the value thus found ranges from 2.7 X 10 7 to 4.9 X 10 7 , with a mean value of 3.8 X 10 7 grams per cm. per second.
The Ricker wavelet
(aka the Mexican hat) is often used in geophysics modelling. The first known
wavelet basis (under a different name) is the Haar basis, for instance in Alfred Haar, Zur Theorie der orthogonalen Funktionen-Systeme, Math.
Ann., vol. 69, pp. 331-371, 1910 (english translation: On the Theory of Orthogonal Function Systems by Georg Zimmermann, with local copy)
Abstract: Die vorliegende Arbeit ist, bis auf unwesentliche Änderungen, ein Abdruck meiner im Juli 1909 erschienenen Göttinger Inauguraldissertation.
Early nearly wavelets include Philip Franklin's
construction of piecewise polynomial orthonormal splines on a bounded
interval (1928), taken to its asymptotics on the whole line by J.-O. Strömberg (1981).
For other earlier wavelet bases (indeed including Haar, Franklin and Strömberg systems), read a nice paper by
Hans G. Feichtinger,
Precursors in
mathematics: early wavelet bases
Abstract: The plain fact that wavelet families are very interesting orthonormal systems for L 2 (R) makes it natural to view them as an important contribution to the field of orthogonal expansions of functions. This classical field of mathematical analysis was particularly flourishing in the first 30 years of the 20th century, when detailed discussions of the convergence of orthogonal series, in particular of trigonometric series, were undertaken. Alfred Haar describes the situation in his 1910 paper in Math. Annalen appropriately as follows: for any given (family of) orthonormal system(s) of functions on the unit interval [0, 1] one has to ask the following questions: convergence theory (sufficient conditions that a series is convergent); divergence theory (in contrast to convergence theory it exhibits examples of relatively "decent" functions for which nevertheless no good convergence, e.g., at that time mostly in the pointwise or uniform sense, takes place); summability theory (to which extent can summation methods help to overcome the problems of divergence);
The concept of "wavelet" in the sense of a small light pulse also
appears in Christian Huygens's (Dutch physicist) light propagation theory. The
term was apparently introduced by Huygens in 1678, but this matter needs
further investigations.
It has been widely recognized that wavelets have aggregated
numerous works from the fields of harmonic analysis, coherent
states in quantum mechanics, electrical engineering or computer
vision.
2005/05/25: i have just discovered that many
french speaking people use "ondulette" instead of "ondelette". It probably comes
form the verb "onduler".
But some googling tells you quite fast that the term is also used for
certain types of "stores" ("Venetian Blind"). This deserves further investigation.
|



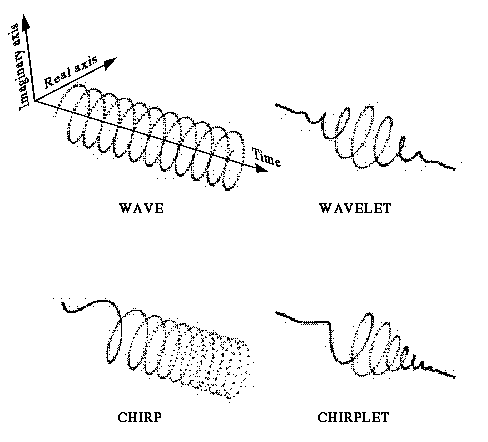
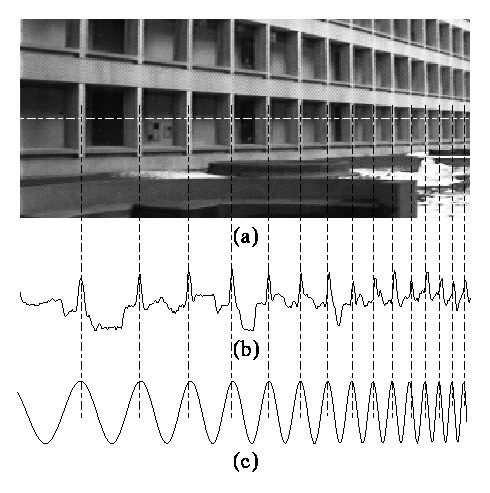


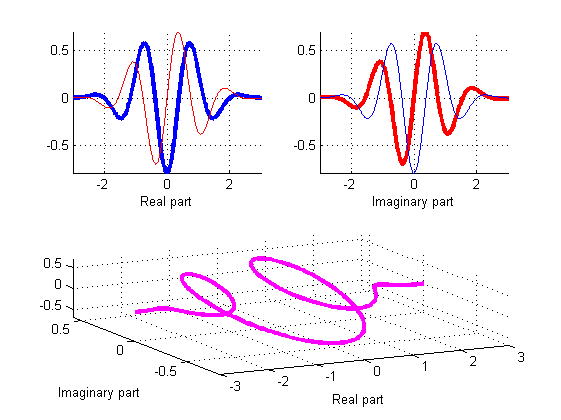 Complex Morlet wavelet with real and imaginary approximate Hilbert pair parts.
Complex Morlet wavelet with real and imaginary approximate Hilbert pair parts.