
| [ Information ] [ Publications ] [Signal processing codes] [ Signal & Image Links ] | |
| [ Main blog: A fortunate hive ] [ Blog: Information CLAde ] [ Personal links ] | |
| [ SIVA Conferences ] [ Other conference links ] [ Journal rankings ] | |
| [ Tutorial on 2D wavelets ] [ WITS: Where is the starlet? ] | |
If you cannot find anything more, look for something else (Bridget Fountain) |
|
|
|
|




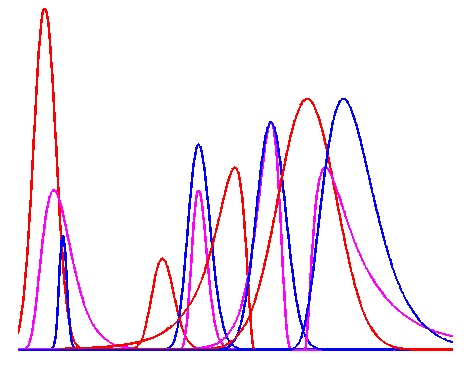
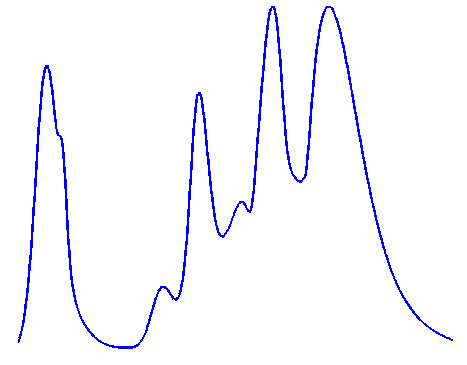
Joint baseline removal or filtering, combined with random noise suppression or cancellation is a important step in analytical data analysis. Analytical data include gas, liquid or ion chromatography; gel electrophoresis; diode array detectors; ultraviolet (UV), infrared (NIR, FIR, IR), Raman or Nuclear Magnetic Resonance spectroscopy, X-ray diffraction or absorption, mass spectrometry. The BEADS toolbox jointly addresses the problem of simultaneous baseline correction and noise reduction, for positive and sparse signals arising in analytical chemistry (Raman, infrared, XRD, etc.), here applied to gas chromatography signals. The baseline is similar to slow-varying trends, signal wanders, instrumental drifts or background offset. The proposed baseline filtering algorithm is based on modeling the series of chromatogram peaks as mostly positive, sparse with sparse derivatives, and on modeling the baseline as a low-pass signal. A convex optimization problems formulated so as to encapsulate these non-parametric models. To account for the positivity of chromatogram peaks, an asymmetric penalty function, similar to a regularized l1 norm is utilized. A robust, computationally efficient, iterative algorithm is developed that is guaranteed to converge to the unique optimal solution.
